Gamma Scalping: A Primer
Trading short-term market movements is challenging. However, option traders who closely monitor volatility can leverage a strategy called gamma scalping to potentially profit from small movements in an underlying asset over time.
Gamma scalping—or gamma or delta-neutral hedging—is an advanced trading approach that requires experience, precision, and a studied viewpoint of the impact of volatility on an underlying security.
Understanding the greeks—specifically, the role delta and gamma play in calculating the price of an options contract—is key to grasping the gamma scalping approach.
Let's look at the financial metrics that influence options pricing, an overview of gamma scalping, and some examples of this strategy.
The greeks and gamma scalping
The options greeks are theoretical measures of an options price's sensitivity to changes in external factors like the price of its underlying security, implied volatility, time until expiration, and interest rates.
Delta, which describes how much an options contract's value is expected to change given a $1 move in the underlying security, is one of the most important greeks to understand before implementing a gamma scalping strategy.
Traders often think of delta as the number of shares of the underlying security they'd need to own for it to mimic the behavior of the option when gamma scalping. The intent of each transaction in this strategy is to re-align the offsetting underlying and options positions to neutralize the net delta.
For example, 40 shares of stock typically behave the same as a long call option with a .40 delta. With all aspects of the model being equal, if the stock price increases by $1, the options premium should theoretically increase in price by $0.40 ($40 in value), and the 40 stock shares will also gain a collective $40 in value.
That brings us to gamma, which reveals how much the delta of an option will theoretically shift with a $1 move in the underlying security. If an option has a delta of .40 and a gamma of .15, its premium would theoretically increase $0.40 on the first $1 increase in the underlying security. This move brings the call option closer to being in the money (ITM) and its delta closer to 1.00. On the second $1 increase, the options premium would theoretically increase $0.55: the sum of delta (.40) and gamma (.15). Gamma decreases as the option gets further ITM because delta cannot exceed 1.00. Gamma is at its highest when the option is at the money (ATM), meaning the strike is equal to the price of the underlying security.
A long options position is essentially a long gamma position. A long option is gamma-positive, meaning rising implied volatility (IV) can be beneficial, as it typically increases the value of both calls and puts. By contrast, a long options position is more likely to lose money when IV falls. Gamma tends to be lower for stocks with relatively high IV and higher on stocks with relatively low IV.
How gamma scalping works
Gamma scalping is a short-term trading strategy that capitalizes on movements in an option's delta. If a trader thinks IV is too low, they may be able to profit by buying long calls and selling the underlying stock, or by buying long puts and purchasing the underlying stock. The number of shares traded should correspond to the delta of the option to create a delta-neutral position. This differs from a protective call or protective put strategy, in which a trader hedges 100 shares of the underlying security with each options position.
Gamma scalping is a strategy most often used by professional traders and transaction costs can be high. Please consider the economic impact of transaction costs, including commissions, fees, margin interest, and taxes before using this strategy.
Typically, the delta of a regular, exchange-traded call option will increase when the underlying stock gains in value, and vice versa—the delta of a put option increases as the stock falls but decreases as the stock rises. Whether a trader is long calls or puts, the delta should move in the direction of the stock price.
Key to this strategy is that both calls and puts have positive gamma. If a trader is long calls and short the stock—or long puts and long the stock—the call will gain more delta when the stock increases in price. And conversely, if the stock decreases in price, the long puts will gain more delta. The aim of gamma scalping is to maintain a delta-neutral position while staying gamma-positive. To achieve this, a trader sells shares in the underlying stock as it increases in price and buys shares as it declines. If they do this whenever the price of the stock changes, the trader aims to buy the shares lower and sell them higher.
If the swings in the underlying stock and the subsequent gamma-scalping gains outweigh the aggregate premiums paid for the options—put another way, if the stock is more volatile than the volatility implied by the gamma—the strategy should be profitable, assuming other factors remain unchanged.
However, if the market is relatively flat and the stock is less volatile than gamma implies, a trader may lose money faster through time-value erosion—known as theta or time decay—than they'll gain from gamma scalping.
Gamma scalping examples
Now that we've explained what gamma scalping is and why traders use this strategy, let's review two trading scenarios to illustrate its practical application.
Detailed breakdown of gamma scalping
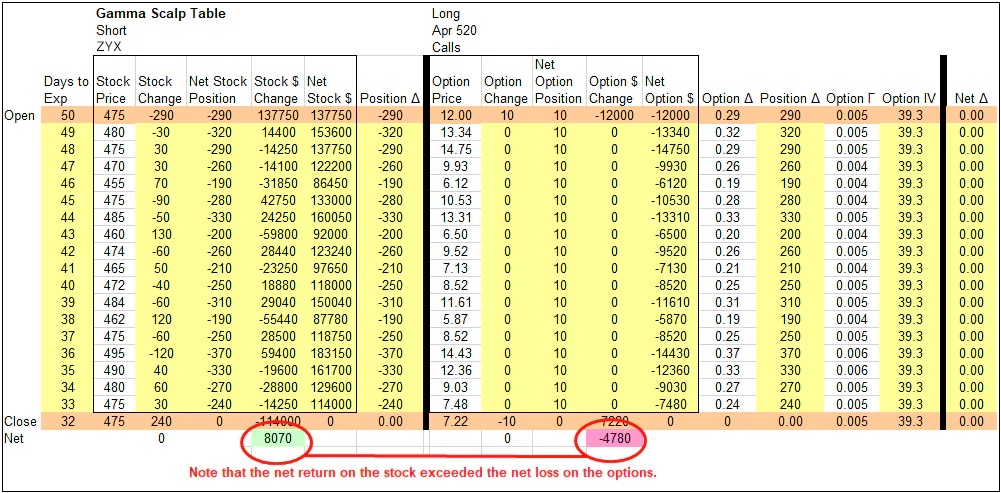
Source: Schwab Center for Financial Research
For illustrative purpose only.
The strategy of buying low and selling high works the same if the stock falls first and then rises. If this happens, a trader could buy back shares as they decrease in price and then sell them again if the price rises. It doesn't matter in which order they do this, as long as they sell high and buy low.
Example 2: Long put and long stock
A trader buys 10 April 60-strike puts for $0.65 per contract on FAHN, with a delta of –.31 and a gamma of .094. To hedge this options position, they buy 310 shares of FAHN at $62. The trade is now delta-neutral—short 310 delta (from the 10 long puts) and long 310 delta (from the purchased shares). However, the trader is net long .94 gamma (.094 x 10 options).
If FAHN decreases 2% in one day to $60.76, the delta of each put will theoretically decrease by approximately the gamma amount of 0.116 (.094 x 1.24 points) to –0.43. Because the trader is long puts, they'll have to buy 120 more shares of FAHN at $60.76 to remain delta-neutral. After this purchase, they'll be short 430 delta (from their 10 long puts) and long 430 delta (from their 430 FAHN shares), maintaining a delta-neutral position.
If FAHN rises back to its previous price of $62, the delta on the puts will increase back to –.31, and the trader could sell 120 shares of FAHN at $62 to remain delta-neutral. Because the sale price of $62 was 2% higher than the purchase price of $60.76, the trader should gain about 2%, or $1.24 per share, on the 120 shares of FAHN (approximately $148). In theory, if this process can repeat enough times before the options expire, the total gains from gamma scalping will exceed the aggregate time erosion of the options in this example.
And remember, it doesn't matter which way the stock moves first if a trader sells high and buys low. This example would be similar if FAHN rose first—prompting the trader to sell shares—and then fell, at which point they bought shares back.
Reverse gamma scalping or negative gamma scalping
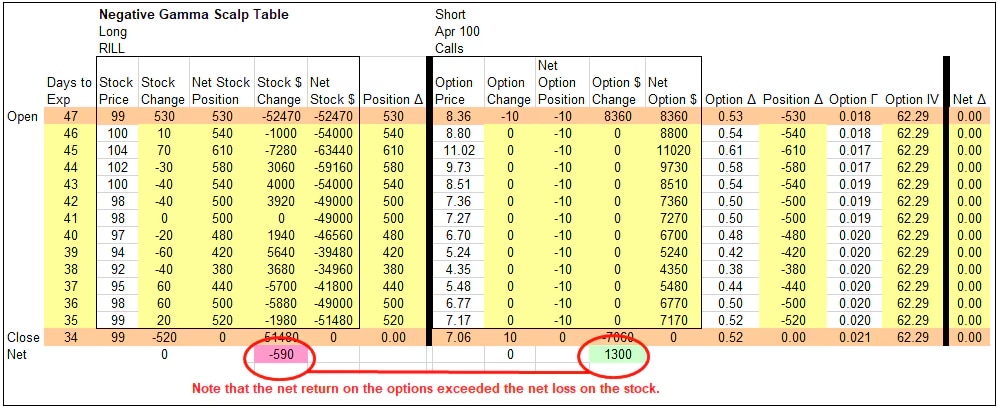
Source: Schwab Center for Financial Research
For illustrative purpose only.
For more information about gamma scalping, or for help using Schwab's options trading tools and platforms, please call a Schwab Trading Specialist at 888-245-6864.