Get to Know the Option Greeks

Option traders often invoke the "greeks." What are they, and more importantly, what can they do for you?
In short, the options greeks refer to a set of calculations you can use to measure different factors that might affect the price of an options contract, but they are theoretical in nature. With that information, you can make more informed decisions about which options to trade and when to possibly trade them.
Let's start with the basic definition of each options greek:
- Delta helps you determine how much an option may move if the underlying stock moves by a dollar, but it can also be used to gauge the likelihood an option will expire in the money (ITM).
- Gamma helps you estimate how much the delta might change if the stock price changes.
- Theta helps you measure how much value an option might lose each day to time decay as it approaches expiration.
- Vega helps you understand how sensitive an option might be to large price swings in the underlying stock.
- Rho helps you simulate the effect of interest rate changes on an option.
Now that you've been introduced, let's explore these calculations in more detail.
Delta
Delta measures how much the price of an option can be expected to move for every $1 change in the price of the underlying security or index. For example, a delta of 0.40 means the price of the option will theoretically move $0.40 if the price of the underlying stock or index changes $1. As you might guess, this means the higher the delta, the bigger the price change.
Traders often use delta to predict whether a given option will expire ITM, meaning its strike price is below (for calls) or above (for puts) the underlying security's market price. So, a delta of 0.40 is taken to mean that, at that moment in time, the option has about a 40% chance of being ITM at expiration. This doesn't mean higher-delta options are always profitable because option buyers have to contest with time decay, which we'll discuss more during the theta section.
Gamma
Where delta is a snapshot in time, gamma measures the rate of change in the delta of an option over time. If you remember high school physics class, think of delta as speed and gamma as acceleration. In practice, gamma is the rate of change in the delta of an option per $1 change in the price of the underlying stock.
In the example above, we used an option with a delta of 0.40. If the underlying stock moves $1 and the option moves $0.40 along with it, the delta is no longer 0.40. Why? This $1 move would mean the call option is now even deeper ITM, so its delta should move even closer to 1.00. Let's assume that as a result delta is now 0.55. The change in delta from 0.40 to 0.55 is 0.15—this is the gamma of the options contract.
Because delta can't exceed 1.00, gamma decreases as an option moves further ITM and delta approaches 1.00. After all, there's less room for acceleration as you approach top speed.
Theta
Theta tells you how much the price of an option should decrease each day as the option nears expiration, if all other factors remain the same. This kind of price erosion over time is known as time decay.
For long calls and puts, theta is always negative, which indicates that the option loses value as time passes. For example, an option with a theta of –0.02 would theoretically lose $0.02 of value every day (including weekends). Like the other greeks, theta doesn't stay the same—it tends to increase closer to expiration, which means options lose value faster as expiration approaches.
Time-value erosion

Source: Options for Beginners: Income Strategies Course
Vega
Vega measures the rate of change in price of the option per one percentage-point change in the implied volatility of the underlying stock. (There's more on implied volatility below.) While vega is not a real Greek letter, it is intended to tell you how much the price of the option should move when the volatility of the underlying security or index increases or decreases.
Rho
Rho measures the expected change in the price of an option per one percentage-point change in interest rates. It tells you how much the price of an option should rise or fall if the risk-free interest rate (U.S. Treasury-bills)* increases or decreases.
Leveraging implied volatility
Implied volatility has a couple of uses beyond vega. Some traders use it to forecast how volatile an underlying stock is expected to be in the future—but it's strictly theoretical. Implied volatility reflected in the price of an option is an inference based on option market participants' expectations of future price moves. Expectations can change depending on upcoming earnings reports, merger and acquisition rumors, pending product launches, etc.
Key points to remember
Figuring out exactly how volatile a stock will be at any given time is difficult, but looking at implied volatility can be a helpful tool in gauging market expectations. Higher-than-normal volatilities warn the underlying security may experience larger-than-expected moves.
However, higher-than-normal implied volatilities are usually more favorable for option sellers, while lower-than-normal implied volatilities are more favorable for option buyers because volatility often reverts back to its average level over time.
By comparing the underlying stock's implied volatility to the historical volatility, you can sometimes get a good sense of whether an option is priced higher or lower than normal.
Putting the options greeks to work
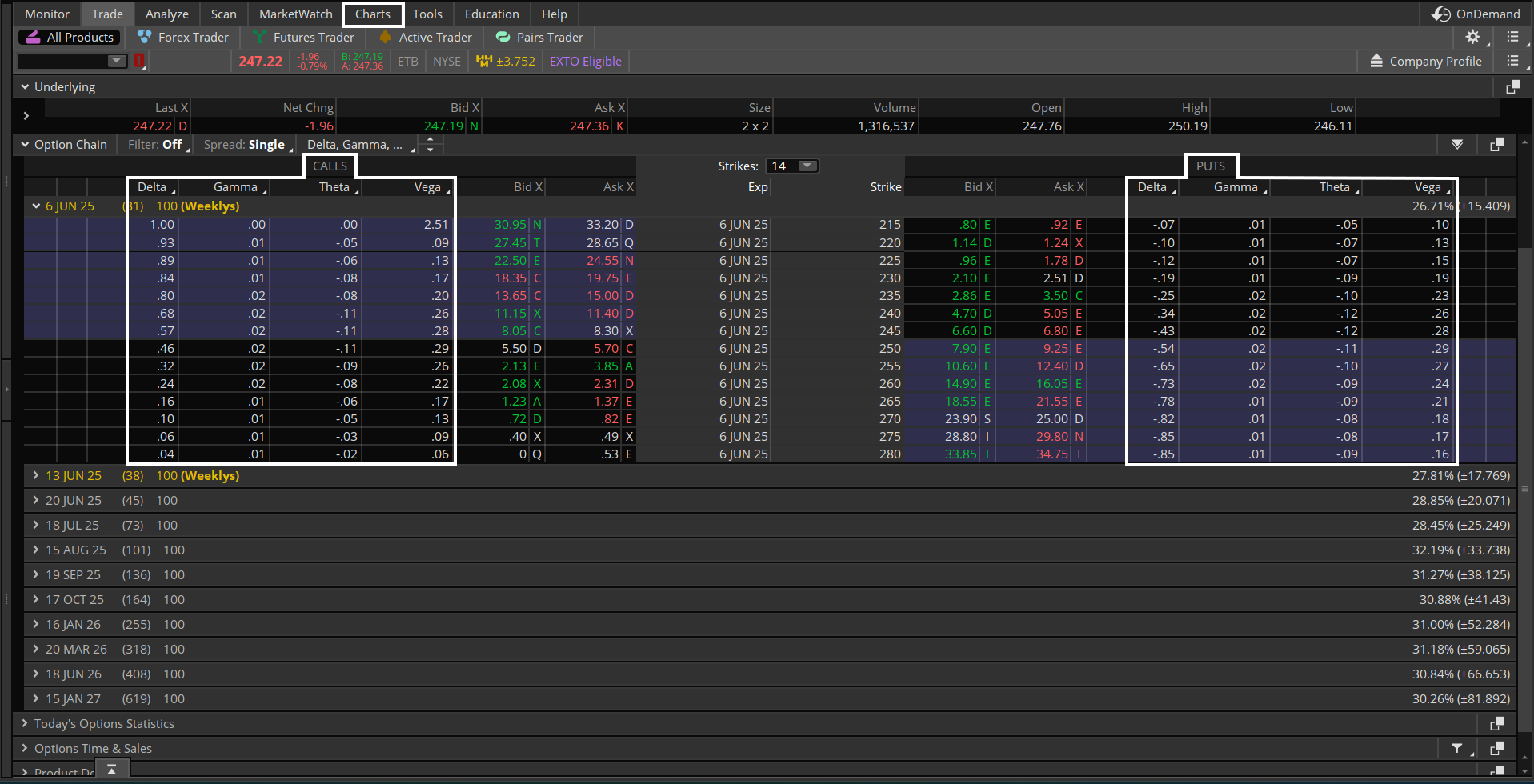
Source: thinkorswim platform
Streaming Greeks in a watch list
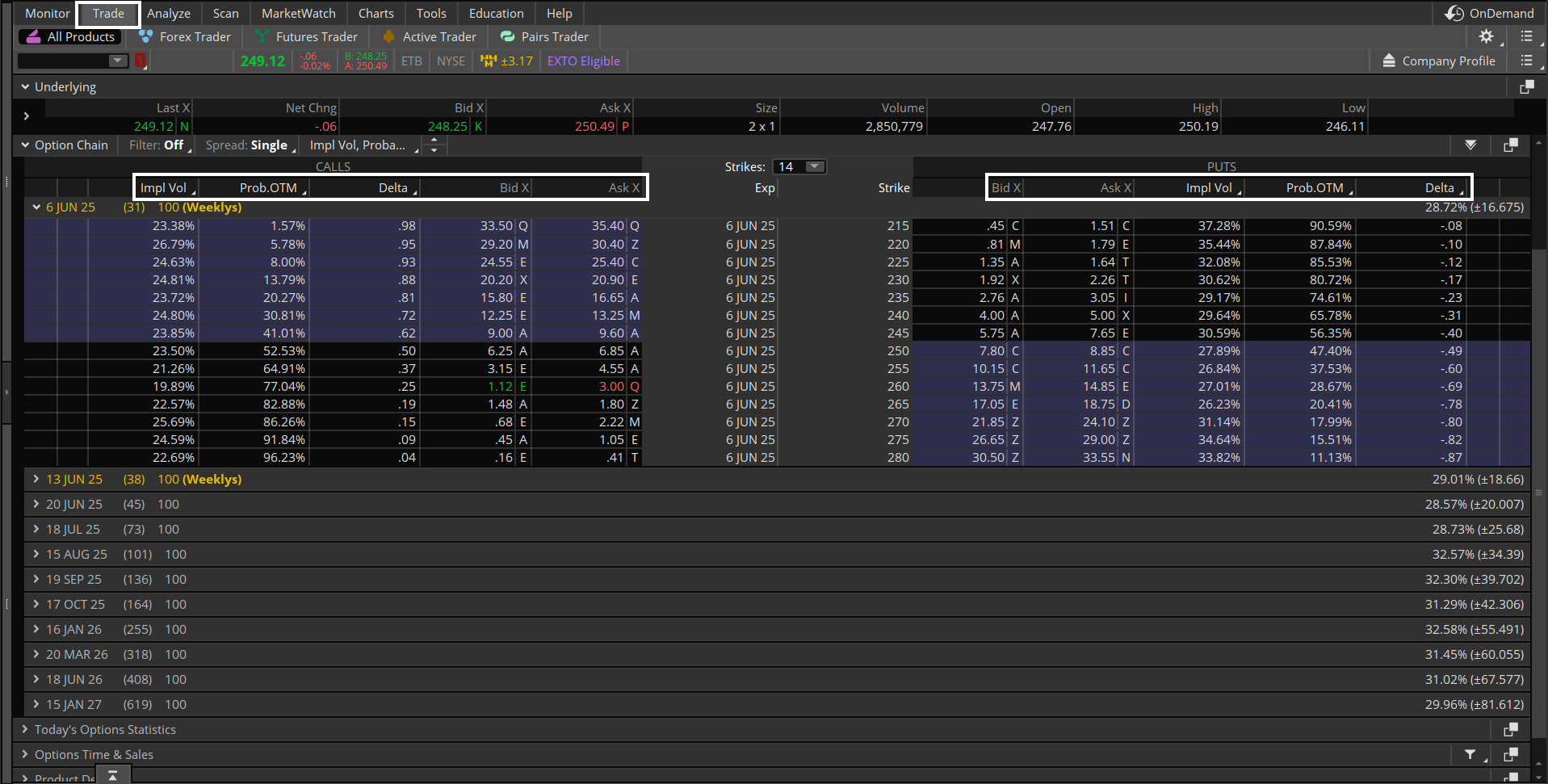
Source: thinkorswim platform
You can arrange the columns to display in any order you like. And, as shown below, you can choose between three of the most widely used pricing models. In addition, the dividend yield and 90-day T-bill interest rate are already filled in. You can use these values or specify your own.
Choose from three widely used pricing models
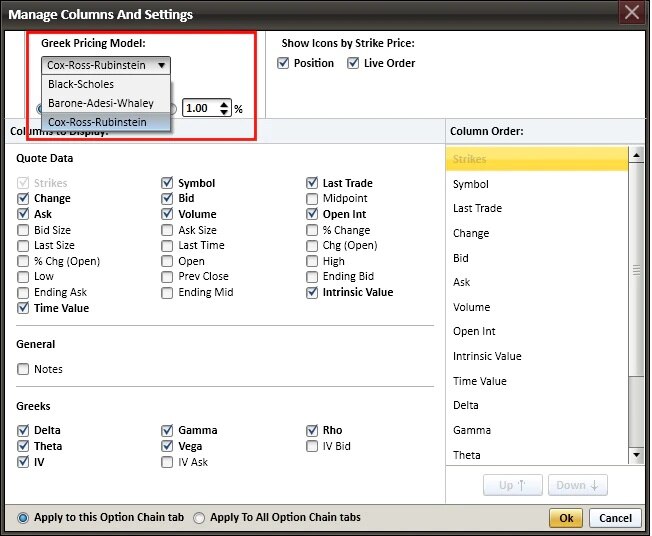
Source: StreetSmart Edge
*The values of "risk-free" U.S. Treasury bills fluctuate due to changing interest rates or other market conditions and investors may experience losses with these instruments.