Options Delta, Probability, and Other Risk Analytics

Probability is generally defined as the likelihood of an event happening, within a certain time frame, expressed as a percentage. With options probability, the event may be the likelihood of an option being in the money1 (ITM) or out of the money2 (OTM), and the time frame might be the expiration of the option.
Armed with the right tools, probability isn't difficult for traders to calculate. One way traders can determine probability is by looking at the options delta3. Among the many pieces of information offered by options delta, many traders look at delta as an approximate percentage chance that an option will be ITM at expiration. Although it's not a perfect science, an options delta calculation can provide a pretty close estimate.
Delta and the Probability ITM feature
In the Option Chain below, the underlying stock is trading around $132, so the 135-strike call is OTM, and its 0.22 delta implies it has about a 22% chance of finishing ITM at expiration. Another way of expressing this is to say the option has about a 78% chance of expiring worthless.
But there's another way Schwab clients can estimate the chance of an option being ITM at expiration: the Probability ITM feature on the thinkorswim® trading platform. The Probability ITM can be added to the Option Chain by selecting a column header, then selecting Option Theoreticals and Greeks > Probability ITM. The calculations may be slightly different from the options delta, but the two readings are generally within a couple percentage points of each other. Either reading can be used to help define the trade's risk. Look up and down the Option Chain at each options delta and Probability ITM and think of it as a probability analysis chart.
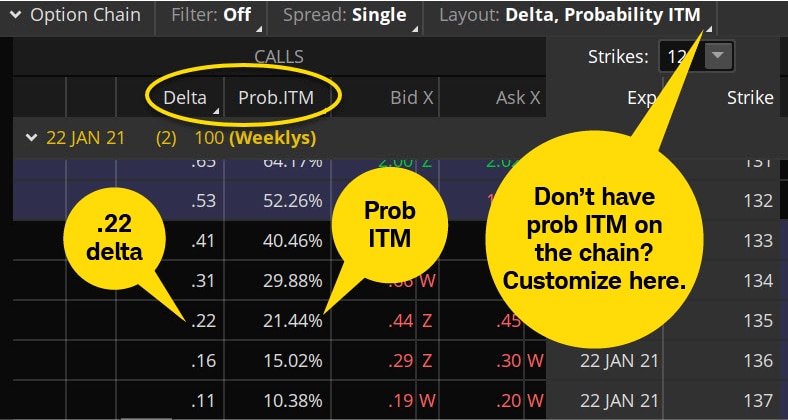
Source: thinkorswim platform
For illustrative purposes only.
A quick side note: Even if an options delta or Probability ITM says 100, there's no guarantee the option will actually finish ITM at expiration. There's always a chance, even if it's a small one, that the underlying stock could have a big enough move to knock something that's deep ITM to a position where it's OTM.
Options spread probabilities
Returning to the example above, suppose that instead of just selling the 135-strike call outright, a trader decides to sell it and also buy the 137-strike call (in trader parlance, this would be "selling the 135-137 call vertical4 spread"). Remember, selling a single option can expose traders to potentially unlimited risk, but selling a vertical spread limits the potential loss to the difference between strikes, minus the premium collected, plus transaction costs.
According to the Option Chain above, the 135-strike call has a delta of 0.22 and the 187.5-strike call has a delta of 0.11. So, using the deltas as probabilities, there's about a 78% chance to keep the entire credit, minus transaction costs, and about an 11% chance the loss will be the maximum amount.
Rather use the Probability ITM numbers? They're about the same. The 135 call shows a 21.44% chance of being ITM, which means it has about an 78.56% probability of being OTM. And there's about a 10.38% chance of the underlying rising above $137 before expiration, which again would result in maximum loss.
Applying the math to decision-making
These numbers assume the position is held until expiration. Depending on a trader's objectives, they could try to close or adjust this trade before expiration. But when structuring a trade and considering adjustments before expiration, understanding these probability calculations can help traders more objectively manage their risk.
Let's look at some basics. First, if an option is currently trading at a price that's ITM, meaning it currently has a delta greater than 0.50, it's more likely to still be ITM at expiration. That's basic options probability theory—the price of the underlying stock fluctuates, but those fluctuations tend to be distributed in a way that's bunched around the current price. Picture a typical bell curve.
Similarly, an option that's currently OTM is less likely to be ITM at expiration. And an option that's right at the money? It's a coin toss as to whether it'll be ITM at expiration; a delta of about 0.50 confirms that.
Comparing an options delta (or other probability calculation) against the price at which a trader could buy or sell an option can help them determine their strategy for entering and exiting options trades.
1In the money (ITM) describes an option with intrinsic value (not just time value). A call option is ITM if the underlying asset's price is above the strike price. A put option is ITM if the underlying asset's price is below the strike price. For calls, it's any strike lower than the price of the underlying asset. For puts, it's any strike that's higher.
2Out of the money (OTM) describes an option with no intrinsic value. A call option is OTM if its strike price is above the price of the underlying stock. A put option is OTM if its strike price is below the price of the underlying stock.
3A measure of an options contract's sensitivity to a $1 change in the underlying asset. All else being equal, an option with a 0.50 delta (for example) would gain $0.50 per $1 move up in the underlying. Long calls and short puts have positive (+) deltas, meaning they gain as the underlying gains in value. Long puts and short calls have negative (–) deltas, meaning they gain as the underlying drops in value.
4An options position composed of either all calls or all puts, with long options and short options at two different strikes. The options are all on the same stock and of the same expiration, with the quantity of long options and the quantity of short options netting to zero.