Out-of-the-Money and In-the-Money Vertical Spreads

The following, like all our strategy discussions, is strictly for educational purposes only. It is not, and should not be considered, individualized advice or a recommendation. Multiple leg options strategies will involve multiple commissions.
Option traders tend to toss around the terms out of the money1 (OTM) and in the money2 (ITM) a lot. And although the definitions are relatively simple, the impact each has on trade results can be quite complex.
Suppose a trader has a bullish bias on a stock or index, and they're contemplating selling an OTM put vertical spread3. What information might be considered when deciding between that strategy or buying an ITM call vertical spread?
First, time decay. When a trader sells an OTM put vertical, that's synthetically the same as buying an ITM call vertical with the same strike prices. Both verticals are theta4 positive, meaning as time passes, all else being equal, time decay5 works for a trader rather than against them.
Second, the potential risk to reward ratio. Say a trader picks their favorite stock XYZ that's trading at $90. They decide to sell the Sep 80/85 put vertical by selling a Sep 85 put and buying a Sep 80 put for a net credit of $1.50. This has the same risk/reward as buying the Sep 80/85 call vertical, which is buying a Sep 80 call and selling a Sep 85 call for a $3.50 debit.
The max profit for the call vertical is the width of the spread, which in this case is $5 minus the $3.50, or $1.50, not including transaction costs. A trader can only get this if the stock price is above $85 at expiration. The max loss for the call vertical is $3.50, which a trader could see if the stock is less than $80 at expiration. It's important to note that the 85 call is at high risk of early assignment because it's ITM. If early assignment happens and the trader does not have an offsetting long stock position in their account, the trader would likely need to exercise their long call to flatten the short stock position.
Side note: Remember the multiplier
For all these examples, remember to multiply the options premium by 100, the multiplier for standard U.S. equity options contracts. So, an options premium of $1 is really $100 per contract.
Now let's look at the max profit and loss from selling the put vertical. A trader's max profit will be the premium, $1.50, which again they'll keep if the stock price stays above $85 through expiration. The max loss will be $5 – 1.50, or $3.50.
If XYZ goes to zero, the max loss on either spread is the same ($350). If XYZ goes to $100, the profit on either is $150. And breakevens? They're the same—both at $83.50. That's why the short put vertical and the long call vertical are synthetically the same. One is created with calls; the other with puts. But as far as risk/reward goes, they're the same.
Traders can experiment with different trading scenarios themselves using the paperMoney® virtual trading platform. From the Analyze tab, enter a symbol, and under Add Simulated Trades, expand the Option Chain of the underlying. Select Vertical from the Spread menu, then choose the put spread (see image below). Next, select Analyze sell trade and then Vertical. Once the order window is populated with the trade details, select the Risk Profile subtab. Do the same with buying the call spread for the same strikes. Compare the two risk profiles to see if they're identical.
Comparing ITM and OTM vertical spreads
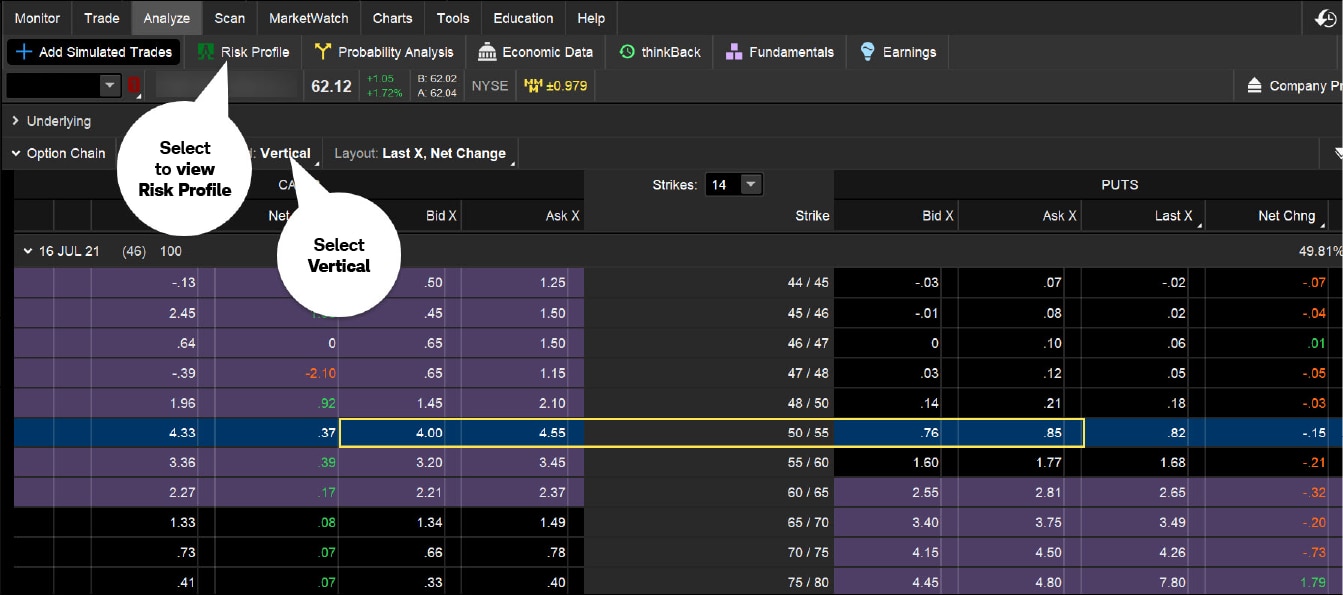
Source: thinkorswim platform
For illustrative purposes only. Past performance does not guarantee future results.
The same…but different
So, what's the difference? It has nothing to do with theory and everything to do with practical trading. It's really about the "tradability" of each.
Liquidity. OTM verticals are typically easier to trade because they tend to be more liquid. That's because more retail participants tend to trade them. And because option traders can sell the OTM call options against their stock position to generate income, there's just usually more activity in them all around. They're also less expensive than ITM spreads. The combination of price plus activity translates into tighter markets for OTM verticals.
Cost of trade. If a trader's short OTM put vertical expires worthless, that's it. They're done. The trader keeps the premium and can move on to the next trade. But the ITM call vertical has a long option that will likely be automatically exercised and a short option that's probably going to be assigned, although it is not guaranteed to happen. That exercise and assignment may have additional fees attached—depending on your broker's commission and fee schedule and potentially on each leg of the trade in addition to any other applicable commissions and contract fees. That can be a big expense to trade the ITM vertical if it turns out to be a winner. The trader could consider attempting to close out the position to avoid any exercise and assignment fees.
1Describes an option with no intrinsic value. A call option is out of the money (OTM) if its strike price is above the price of the underlying stock. A put option is OTM if its strike price is below the price of the underlying stock.
2Describes an option with intrinsic value (not just time value). A call option is in the money (ITM) if the underlying asset's price is above the strike price. A put option is ITM if the underlying asset's price is below the strike price. For calls, it's any strike lower than the price of the underlying asset. For puts, it's any strike that's higher.
3The simultaneous purchase of one put option and sale of another put option at a different strike price, in the same underlying, and in the same expiration month.
4A measure of an options contract's sensitivity to time passing one calendar day. For example, if a long put has a theta of –0.02, the options contract's premium will decrease by $2.
5Time decay, also known as theta, is the ratio of the change in the price of an option to the decrease in time until expiration. As an option approaches its expiration date without being "in the money," its time value erodes because of the reduced probability the option will be profitable.